 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Системы регулирования
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 [ 103 ] 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193
Критическое время запаздывания т. найдем из условия равенства фазовой частотной характеристики разомкнутой системы при частоте (о = (Ос величине-я
ф ( laquo;с) = - arctg aj - (ОсТк = - п.
Из последнего уравнения находим
- lt;0с Vk - 1
331. Передаточная функция разомкнутой системы автоматического управления имеет вид
о(Р)р(1 + Гр)
где К = 20 сек~ - общий коэффициент усиления разомкнутой системы, Г = 0,1 сек - постоянная времени. Последовательно ъ кана.?! управления включается звено чистого запаздывания, имеющее передаточную функцию e-Р, где т -время запаздывания. Требуется найти Критическое время запаздывания т, при котором зам- кнутая система автоматического управления находится на границе устойчивости, и частоту незатухающих колебаний (Ок. , . Ответ. -а)к=12,5 сек~, Тк = 0,11 сек.
332. Решить предыдущую задачу, если постоянная времени Г = 0.
Ответ. (Ок = 20 се7с-\ = 0,78 сек. 333. Передаточная функция разомкнутой системы имеет вид
С помощью логарифмических частотных характеристик определить критическое время запаздывания Тк, если коэффициент усиления разомкнутой системы К = 30 сек~, постоянные времени. Ti = 0,025 сек и Га = = 0,2 сек.
Решение.. Асимптотическая л. .а. х. системы приведена на рис. 193. Частота среза разомкнутой системы
Юс = 12,6 сек . Фазовая частотная характеристика при частоте со = Юс и критическом времени запаздывания
j - Гч-. 1 1 1 1 h 1 1 1 1 ) 1 1 Н 1 1- | |||
Н- / | -(-1-\-fl 1 11 -1 ~ 1 1 г г 1т ) if} \ f/Ji | ||
-20- | |||
Рис. 193. Асимптотическая л. а. х. к задаче 333. должна пересекать линию 11;= -п. Поэтому
ф (Шс) = - Y - arctg (ОсГ1 - arctg (Осг - cOcT = - я. Отсюда находим
Y - arctg laquo;ОсГ, - arctg сосГг
laquo;Ос
= 4,8 10 сек.
334. Определить критическое время запаздывания т системы, структурная схема которой приведена на
Рис. 194. Структурная схема к задаче 334.
рис. 194. Общий коэффициент усиления разомкнутой системы К = ,ф,ф,==Ъ, постоянные времени апериодических звеньев Г, = 5 сек и ТОА сек. Ответ. Т((= 1,4 сек.
335J
sect; 9.1. СИС.Тр.МЫ ,С ВРЕМЕННЫМ ЗАПАЗДЫВАНИЕМ
335. Передаточная фун1сция разомкнутой системы имеет вид .
Woip) р(1 +7-V)
где /С = 2 сек~, Г = 0,1 сек. Для достижения устойчивости системы последовательно в канал управления вводится звено чистого запаздывания с передаточной функцией е . Определить, при каких значениях времени запаздывания т замкнутая система устойчива. Р ё ш е и и е. Результирующая передаточная,функция
разомкнутой системы W (р)= Woip) е-Р jj..
Асимптотическая л. а. х. системы приведена на рис. 195. Замкнутая система будет устойчивой, если
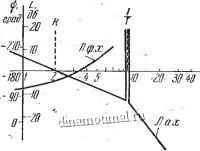
ui.ce/f
Рнс. 195. Асимптотическая .п. а. х. и ф. х. к за.аче 335.
Л. ф. X. пересекает линию = - я в дпапазоие частот K-i-y-. Критические значения времени запаздывания Тк находим из след sect;/ющих уравненпй:
iL ft L
Отсюда
f к тл.ч = = 0.79 сек, т,( niin = ==0,\% сек.
Замкнутая система.устойчива, если выполняется следующее неравенство: 0,16 сек lt;т lt; 0,79 се?с.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 [ 103 ] 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 |