 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Системы регулирования
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 [ 118 ] 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193
Решив уравнения (6) и (7) совместно, получим
(ТоР +1)рЬ=- Mo при + Ь, (8)
iToP-il)pb = koe gt;o при -Ь, (9)
(7оР+1)р = 0 при 6. (10)
Рассмотрим уравнение (8):
0-+-= - коЩ. (И)
Введем-обозначения х = amp;, У и уравнение (II) перепишем следующим образом;
n + y==-h. (12)
Для исключения времени из уравнения (12) разде-
ЛИ.М его н а ~- = у. Получим . . ,
dy I ko lt;uo ,
... dx~ То Тоу . . . .,. . .
или после разделения переменных
d---ody-dy: -л (13)
проинтегрировав уравнение (13), получим уравнение фазовых траекторий
х= - ТоУ+Токо(Оо1п{у + ко amp;о)+С1 при х gt; + Ь. (14)
Проделав аналогичные операции с уравнениями (9) и (10), получим для них
х= - ТоУ- 7оо reg;оЩу- о laquo;о) + Сг при х lt;- Ь, (15) х--ТоУ + Сз при \х\ lt;Ь. (16)
Поставив в уравнения (14) -(16) численные значения-параметров, получим
jc= - 10i/ + 221n(2,2 + i) + C, при .Jc gt; + b, (17)
л;= - 10-221n(2,2-) + C2 при x lt;-b, (18)
л:==-10/ + Сз при \Х\ lt;Ь. (19)
По уравнениям (17) -(19) на рис. 229 построен фазовый портрет всей системы. Там же выделена фазовая
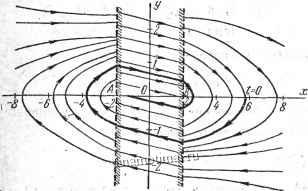
Рис. 229. Фазовые траектории системы регулирования температуры к задаче 383.
траектория, соответствующая начальным условиям: при f = О 0 = 5,7 deg;, 0 = 0. По виду фазовой траектории можно установить, что процесс в системе заканчивается немного больше, чем за один период колебаний. Переходный процесс в системе можй- закончиться в любой точке отрезка АВ.
384. Исследовать процессы в системе регулирования температуры, рассмотренной в задаче 383, при условии, что поляризованное реле обладает статической характеристикой, изображенной на рис. 230. Численные значения параметров: Ь = 2 deg;, (Оо = 0,22 рад1сек.
Ответ. Уравнения фазовых траекторий в области 7 и в области (рис. 231) следующие:
а: = - 10/-Ь 22 In (2,2 + f/)-h С
д;= - 10f/-221n(2,2-f/) + C2. .
(Off | |||||
Рис. 230. Статическая характеристика нелинейного звена к задаче 384.
Переключение привода происходит на прямых АВ и CD. В системе при любых начальных условиях устанавливаются автоколебания. Амплитуда колебаний температуры ttf) != raquo; 5 deg;, амплитуда колебаний скорости изменения температуры а* 1,2 град/сек.
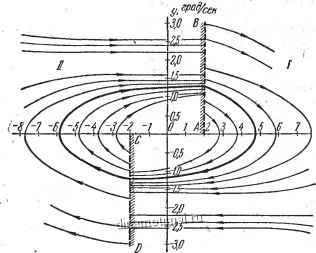
Рис. 231. Фазовые траектории системы регулирования темпе- ратуры к задаче 384.
F(u)
Рис. 232. Система стабилизации ИСЗ и статическаи характеристика управляющего устройства к задаче 385.
385. Исследовать устойчивость системы стабилизации искусственного спутника Земли (ИСЗ), схема которой изображена на рис. 232 а, 6. ,
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 [ 118 ] 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 |