 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Системы регулирования
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 [ 127 ] 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 
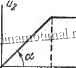
екая характеристика нелинейного звена изображена на рис. 250.
Ответ. В системе устанавливаются автоколебания с амплитудой Л 6,3 и частотой Q= 10 сек *
А, = 6,3 sin 10.
- 401. Найти область устойчивого состояния равновесия и область автоколебаний и определить амплитуду н частоту автоколебаний для следящей системы, схема.которой изображена на рис. 209, при учете нелинейности типа насыщения в предварительном усилителе и отсутствии релейного усилителя и обратной связи по напряжению тахогенератора.
Исходные данные: постоянная времени усилителя Ti = 0,1 сек, электромеханическая постоянная времени двигателя Г2= 1 сек, общий коэффициент передачи линейной части системы k=20 сек~, коэффициент передачи чувствительного элемента ki = 50 в/рад, статическая характеристика уси- лителя изображена на рис, 251. Исследование провести для 2 = 1 и 2 = 2.
Рис. 251. Статическая характеристика усилителя следящей системы к задаче 401.
Рис. 252. Структурная схема следящей системы к задаче 401.
Рещение. Составляем структурную схему системы (рис. 252). Согласно этой схеме дифференциальное уравнение линейной части системы при amp;i{0 = 0 запишем в виде
(Г2Р+-Мз, (1)
где. к.куНф.. : . . ; . .
Дифференциальное уравнение нелинейного звена имеет ВИД
{Tip+l)u2kyUi. (2)
Коэффициент усиления усилителя ky является нелинейной функцией, заданной графически (рис. 251). Поэтому согласно методу гармонической линеаризации запишем для него гармонически линеаризованное выражение
k=.g{a) + -p, (3)
где коэффициенты гармонической линеаризации для характеристики с насыщением имеют значения (см. приложение 28)
q{a) = k2 при аЬ,
9(a) = (arcsinA + A/ rr) при аЬ, (4) . 9( laquo;) = 0.
Из уравнений (1) -(3) получим лршеаризованное уравнение замкнутой нелинейной системы
liT,p+l){T2P + l)p + k q{a)]uy = 0, (5)
которому соответствует характеристическое уравнение
TiT2P + {T, + T2)p + P + k Q{a) = 0. (6)
Для отыскания условий существования периодического решения
ы, = А sin Qt (7)
из характеристического полинома после подстановки р = }т выделим вещественную и мнимую части и приравняем их нулю,-
У(ш) = (й(1-7,Г2(й2).
Частота периодического решения находится из второго уравнения (8)
sect; 13.1. АЛГЕБРАИЧЕСКИЕ СПОСОБЫ
Б89
Из первого уравнения (8) с учетом (9) получим формулу, связывающую амплитуду периодического решения с параметрами системы
(10)
Для исследования устойчивости периодического решения найдем частные производные от выражений (8):
дХ\* да )
дд (А) дА
(Ж)- -2О(7, + laquo;=-2.1и=й-=-0,
,696,
(II)
(1)= 1-37,r2Q2= 1-3=-2.
Для устойчивости периодического решения (7) требуется, чтобы выполнялось не-равенство
(дХУ IdYV \dal и raquo; j
. -(S(W gt; deg;.
или, с учетом НИИ (И),
выраже-
дд{А) дА
gt;0,
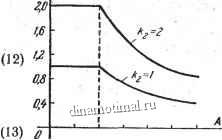
0.S 1.0 1 г.о 2 3.0
Рис. 253. Зависимость коэффициента гармонической линеаризации от амплитуды колебаний к задаче 401.
Т. е. частная производная (Л)
-должна быть отрицательной.
Для определения знака этой производной по выра- gt;кёнию (4) для q{A) построим график (рис. 253), согласно которому
lt;0 при. А gt;Ь. (14)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 [ 127 ] 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 |