Динамо-машины  Системы регулирования 

1 2 3 4 5 6 7 8 9 10 11 12 13 [ 14 ] 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193

гл. 1. УРАВНЕНИЯ Н ПГРКДАТОЧНЫЕ ФУНКЦИИ

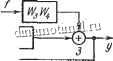
Решение. Вначале получим передаточную функцию автоматической системы по возмущению Of{p), для чего преобразуем структурную схему рис. 27, а. Перенесем сумматор 2 через звено и заменим Wi, W2 одним

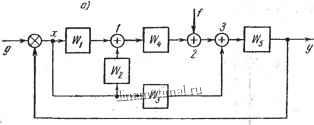
Рис. 27. Структурные схемы к задаче 46.

звеном (рис. 27, б). Найдем передаточную функцию разомкнутой системы по задающему воздействию

и по возмущению

Тогда

ФЛр)

Y{p) Wf (р)

F(p) l + W (p) ap + a,p2 + ajp + 03

где У(р), /(p) -изображения управляемой величины y{t) vsr возмущения f(f), p = с +/со - комплексная переменная, d = KJ d, = 5, aT.Tl а, = Г-ЬГ/з.

laquo;2 = 1 + 3 + hb + kJ amp;Tx, G3 = I -1- /jgfej + kihk..

laquo;1

sect; 1.4. СТРУКТУРНЫЕ СХЕМЫ И ИХ ПРЕОПРАЗОВАНИЕ

Отсюда искомое дифференциальное уравнение имеет

{аор + aip2 + ар + а) у (t) = {dop + d,) / (/), р =

dt

47. Найти следующие передаточные функции автоматической системы, структурная схема которой

I 3 г

к raquo;

I 3 2

Р.ис; 28. Структурные схемы к задаче 47.

изображена на рис. 28, а: разомкнутой системы по задающему воздействию W(p) и по возмущению Wipft

БО гл. t. УРАВНЕНИЯ и ПЕРЕДАТОЧНЫЕ ФУНКЦИИ [48

основную Ф{р), ПО возмущению Of(p) и относительно, ошибки по задающему воздействию Oip)-

Решение. Преобразуем структурную схему рис.-28, а (см. рис. 28, б, е и г). По структурной схеме рис. 28, г найдем

W (р) = Г1ГИ- (I + + Г5, Wf (р) = WsW

fyP- l + WiW2 + {l + WiW2W3)Wi + Wi .

l + WtW + il + WiWWs) Wi+Ws

48. Найти дифференциальные уравнения автоматической системы, структурная схема которой изображена на рис. 28, а, относительно управляемой величины y{t) по задающему воздействию g{t) и по возмущению f{t), а также относительно ошибки x{t) по задающему воздействию g{t) и по возмущению f{t), если Wi(p) = /Ji,

( gt; = т;1 з(Р)-А., Г4(р) = . wM=jy

Ответ.

Dip)y{t) = {bop + biP + b2)g(t), . D{p)y(t)=={dop + dip + d2)f{tl D{p)x{t) = icop + CiP + C2p)g{t), D{p)x{t)=-(dop + dip + d2)f{t),

где характеристический полином системы

jD (р) = йоР+ aiP + Й2Р + laquo;з; laquo;о = Со, ai = bo + Ci, a2 = amp;i4-C2, аз= amp;2; amp;о = i№72 + ПГг. bi = -f -Ь Ь + feifefez + klTi,

amp;2= 1-bfeifeyfe3 + №;

ео=А;ГГ1Г2, с, = -t-7-2). C2 = A;j;