 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Системы регулирования
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 [ 38 ] 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193
Передаточная функция разомкнутой системы имеет комплексные коэффициенты. Поэтому для определения устойчивости необходимо построить а. ф. х. в диапазоне частот - оо -т- + оо.
А. ф. x. системы приведена на рис. 96. Из рис. 96 видно, что а. ф. x. разомкнутой системы не охватывает точку (- 1, 0). Следовательно, двухканальная следящая система устойчива. ,
148. Структурная схема системы приведена на рис. 97. Параметры системы равны: /С = 20 сек , Т - 1 сек, а = 2. Определить устойчивость системы.
р(Мр) | ||||
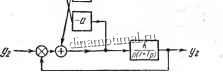
Рис. 97. Структурная схема двухканальной счедящей системы к задаче 148.
Ответ. Система неустойчива. Следует отметить, что при отсутствии перекрестных связей (при а~0) система устойчива при любых,/С gt;0 и 7 gt;0.
sect; 3.4. Определение устойчивости по логарифмическим частотным характеристикам разомкнутой системы
149. Передаточная функция электромеханической следящей системы в разомкнутом состоянии имеет вид
Р р(1+ТиР){\+Тур)
где К = 75 сек-\ Гм = 0,02 сек, Гу = 0,005 сек.
Определить устойчивость замкнутой системы по логйрифмическим частотным характеристикам разомкнутой системы. . -
ц raquo;1 sect; 3.4. ЛОГАРИФМИЧЕСКИЕ ЧАСТОЛ1ЫЕ ХАРАКТЕРА КИ 123
Решение. Устойчивость системы будем определять по асимптотической л, а. х. и л. ф. х. Частоты излома асимптотической л. а. х. равны
0,005
= 200
\ Низкочастотная асимптота л. а. х. пересекает ось цЛ лог при частоте
- 0D = / lt; = 75 сек-.
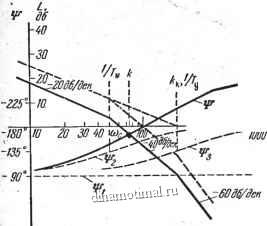
По этим данным строим асимптотическую л, а. (рис. 98). с1:,азовая частотная характеристика равна
где 11),(с))== -90 deg;, il2( laquo;)) = -arctg (оГ -arctg 0,02 lt;й, фз lt; lt;о) = - arctg ГуЮ = rctg 0,005(0.
Л i i i i д-й). сен
Рис. 98. Асимптотические л. а. х. и л. ф. х. к задачам 149 и 152.
Графики функции i])2( laquo;)) и г])з((о) строим с помощью шаблона.
Л. ф. x. получаем графическим сложением функций iH, ф2(ю), Фз( laquo; gt;) (см. рис. 98).
л. ф. X. пересекает линию 115 = -180 deg; при отрицательных значениях асимптотической л. а. х. Следовательно, замкнутая система устойчива.
В данной задаче л. ф. х. является монотонной функцией от частоты (о, поэтому задачу можно решить без построения л. ф. х.
После построения асимптотической л. а. х. опреде-; ляем частоту среза разомкнутой системы со = copy;с = 60 ce,-i (см. рис. 98).
Значение фазы при частоте среза ,
яр (и,) = 90 deg; - arctg (0,02 60) - arctg (0,005 Щ =
= -157 deg; gt;-180 deg;.
Следовательно, замкнутая система усайчива.
150. Определить устойчивость си;бт€мы, рассмотренной в задаче 149 при / у = O.OQS сек, Г =.0,02 сек,. / lt;- = 300 сек-К
Ответ. Система неустойчива.
151. Передаточная функция разомкнутой системы имеет цид
W(n\. Kjl+rp)
Р р(1+Т,ф)(1+Тур)
где /С = 300 сек-\ Г = 0,02 сек, Гу = 0,005 сек, т = 0,0045 сек. Определить устойчивость системы. Ответ. Система устойчива-.
152. Для электромеханической следящей системы, рассмотренной в задаче 149, определить значение добротности системы, при котором система находится на колебательной границе устойчивости.
Решение. Логарифмическая фазовая характеристика определяется выражением
ф (со) = ifi (со) + 4l32 (со) + -фз (со),
где ф) (со) = - 90 deg;, % (со) = - arctg соГ, Фз = - arctg соГу.
Графики функций izi) и фз(со) строим с помощью шаблона. Л. ф. х. получаем графическим сложением характеристик il)i((i)). {(i)) и gt;1з(а gt;) (см. рис. 98).
Система находится на колебательной границе устойчивости, если л. а. х. пересекает ось частот при частоте пересечения л. ф. х. линии ч}} = -180 deg;, 0 = 100 сек .
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 [ 38 ] 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 |