 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Системы регулирования
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 [ 90 ] 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 
х.сен

-Ofi-0A-O,Z О 0,2 0,4 Цбт,се/(
Рис. 177. Корреляционная фуик- Рис. 178. Коррсняциониаифуик-ция к задаче 293. ция зжспоггеицнального вида.
Ответ. Нормированная спектральная плотность при (Оп (о (й равна
(0)) = -=- = .
Нормированная корреляционная функция
R (т) sill Юдт
Р(т) = -Значение р (т) при т = О
(ОпТ
p(0) = iitniHl = l.
295. В результате обработки осциллограммы стационарного случайного процесса с математическим ожиданием (средним значением), равным нулю, получено выражение для корреляционной функции
R{x) = De-\
где D = 100 -дисперсия и м-= 5 сек - параметр затухания. Корреляционная функция построена па рис. 178. Определить спектральную плотность и построить ее график.
Решение. Спектральная плотность может быть найдена согласно интегралу Фурье [2]
4-00
5(0))= R (т) е- d%
294. Для предыдущей задачи определить-нормированное значение спектральной плотности и корреляционной функции.
Последний интеграл для удобства желательно разбить на два: - .
г о
5( laquo;)) = / gt;
g(ji-/ lt;o) t dt +
g-(H+/ lt;o) x dx
2цР
Г = ~ = 0,2 сек.
Подстановка численных значений дает
е./ \ 40
Спектральная плотность построена на рис. 179.
Sfcu) | |
- т. 1 i 1 . | Г . ( |
-6 -4 -г о
Рис. 179. Спектральная плотность, соответствующая корреляционной функции па рис. 178.
296. Решить предыдущую задачу, если рассматриваемый стационарный случайный процесс имеет среднее значение (математическое ожидание) х = Б. Построить графики корреляционной функции и спектральной пло1-ности.
Ответ. Средний квадрат случайной величины
j?=D + A-== 100 + 5= 125.
Корреляционная функция
Л (т) = gt; + 2 = 100в-5 1 + 25.
looj- | ||
/50- | ||
1 1 1 | i г. | |
-Ofi-Dfi-QZ О аг Dfi 0,6t,cen S((o)\
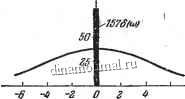
Рис. 180. Корреляционная функция и спектральная плотность к задаче 296.
297. В результате обработки осцилограммы -случайного стационарного процесса с математическим ожиданием, равным нулю, получено выражение для корреляционной функции:
7?(T) = Z)e-icospT, (1)
где Z) = 40 - дисперсия, ц = 0,5 сек - параметр затухания (коэффициент нерегулярности) и р = 2 сек - резонансная частота. Корреляционная функция изображена на рис. 181. Найти аналитическое выражение и построить график спектральной плотности. Ответ. Спектральная плотность
S(( raquo;) = tiD
Ln + (P- laquo;))2 f ц= + (р + а)Ч-
Спектральная плотность .
S( laquo;) = 2nx6(c.) + -=l57Mc.)+T+W gt;
где б (ш) -единичная импульсная функция. Графики построены на рис. 180.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 [ 90 ] 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 |