 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Электроприводы
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 [ 81 ] 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130
где F- промежуточная функция. На основании (6:34)
F=v-Xo (v + ,0, (6.44)
где - произвольная постоянная или множитель Лагранжа. Производя дифференцирование этой промежуточной функции но (6.29), получим уравнение Эйлера в конкретизированной форме:
2\%~2\./+\=Q. (6.45)
Почленное интегрирование этого уравнения, предварительно умноженного на и на ах, дает:
{Г-? + = Л. (6.46)
Поскольку j==v+!J,c, то имеем следующую взаимозависи-MOCTiij между током и скоростью вращения якоря:
P + 2v-i=--Y{A- gt;). (6.47)
Уравнения (6.45) - (6.46) справедливы для любой зависимости статического момента от скорости. Для привода с постоянным моментом сопротивления дифференциальное уравнение Эйлера принимает вид
2 gt;oS+l=0. (6.48)
Его первый интеграл
*оЙГ + = - (6.49)
Второй интеграл
v = Л2 + ЛlX-, (6.50)
где Л] и постоянные интегрирования.
Вторая искомая функция - ток якоря, определяемый нэ lt;6.42):
= + (6.51)
Проверка показывает, что условия Якоби и Лагранжа удовлетворяются. Выражение (6.50) показывает, что оптимальная зависимость скорости вращения от времени носит параболический характер. Из (6.51) следует, что в оптимальном режиме ток якоря должен изменяться во времени линейно. Постоянные интегрирования Л1 и Лг находятся из граничных условий: т=0 и т==Г, что соответствует v=vi и v=V2.
Во многих случаях переходные режимы отличаются нулевы-
ми граничными условиями vi=V2=0. при этом At= и Л2=0.
Постоянную ко определяют из условия заданного перемещения механизма Од или заданных потерь энергии Q:
откуда
) - Д - бяд 3 Яд
Если заданы потери энергии
Знак перед радикалом берется положительным, исходя из условия Лежандра. Заменяя произвольные постоянные их значениями для нулевых граничных условий, получаем:
i = V-c.o + io (l -
v = t gt; (6.52)
По заданным потерям в якоре
В случае заданного перемещения а
На рис. 6.24,0! приведены оптимальные функции времени: линейная и параболическая для тока и скорости якоря. В режиме оптимального управления существует определенная зависимость между током и скоростью вращения якоря (6.47), из которой следует; что ,
Эта параболическая зависимость при !J,=const изображена на рис. 6.24,6. Ток якоря, достигающий наибольших величин в области малых скоростей вращения, уменьшается по мере ее увеличения. Такой характер изменения тока с точки зрения коммутации - можно считать вполне приемлемым. Подстановка в (6.37) квадрата тока и интегрирование позволяют установить взаимосвязь между потерями энергии, перемещением и вре менемс
Q = - + lc.oT. (6.53)
Если заданы перемещение а и время Т, то эта формула дает минимальные потери энергии; в случае же заданных потерь энергии и времени она определяет максимальное перемещение а, и, наконец, когда перемещение и потери заданы, она выражает
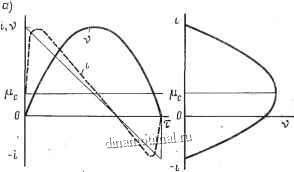
Рис. 6.24. Оптимальные характеристики двигателя с постоянным магнитным потоком при постоянном статическом моменте сопротивления: а) i, м = 1р(т) б) г = ID (v)
минимальное время. Для законов управления, отличных от полученного оптимального, показатели работы электропривода снижаются. Так, в случае прямоугольной кривой тока (t = -(-io при разбеге и (=-io при торможении) на основании (6.37) и (6.36)
имеем: Q = ilT, а =
и окончательно Q = 16 Потери же
7-3
энергии (6.53) в оптимальном режиме Q=I2-y3.
Из этих соотношений следует, что при одинаковой производительности потери энергии при оптимальном управлении на 33% меньше, чем в случае прямоугольной кривой тока. Можно также показать, что при управлении током по закону синуса
1,п sin -уг- 1
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 [ 81 ] 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |