Динамо-машины  Сигналы и спектры 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 [ 114 ] 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358

Принятый seiaop г -

Синдром S

Ошибочная комбинация е \в\

Принятый вектор

Исправленный результат U

Логические элементы

исключающее ИЛИ

Логические элементы И

ul u2 из щ Us ue

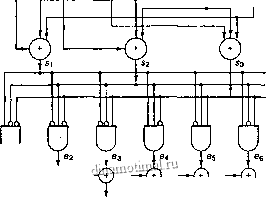
Puc. 6.12. Схема реализации декодера для кода (6, 3)

Декодеру не нужно выдавать полное кодовое слово; на выходе у него должны быть только биты данных. Поэтому схема на рис. 6.12 упрощается за счет удаления заштрихованных элементов. Для более длинных кодов такая реализация намного сложнее; более предпочтительной методикой декодирования является последовательная схема, а не рассмотренный здесь параллельный метод [4]. Важно также подчеркнуть, что схема на рис. 6.12 позволяет определять и исправлять только модели кода (6,3) с одним ошибочным битом. Исправление моделей с двумя ошибочными битами потребует дополнительной схемы.

6.4.9.1. Векторные обозначения

Выше кодовые слова, модели ошибок, принятые векторы и синдромы обозначались как векторы U, е, г и S. Для упрощения записи индексы, сопутствующие конкретному вектору, в основном, опускались. Хотя, если быть точным, каждый из векторов и, е, г и S должен записываться в следующем виде;

Xj={Xx,X2, ...,х ... )

Рассмотрим диапазон индексов у и i в контексте кода (6, 3), приведенного в табл. 6.1. Для кодового слова Uj индекс j = 1, 2* показывает, что имеется 2 = 8 отдельных кодовых слов, а индекс i= 1,л демонстрирует, что каждое кодовое слово составлено из laquo; = 6 бит. Для исправимой модели ошибки е, индекс у= 1, 2 означает, что имеется 2 = 8 образующих элементов классов смежности (7 ненулевых исправимых моделей ошибки), а индекс i = 1, л указывает, что каждая модель ошибки составлена из п = 6 бит. Для принятого вектора г, индекс j= 1, 2 показывает, что имеется 2* = 64 п-кортежей, прием которых возможен, а индекс /= 1, п указывает, что каждый принятый л-кортеж состоит из л = 6 бит. И наконец, для синдрома S, индекс j = 1, л - А- означает, что каждый синдром состоит из л - А- = 3 бит. В этой главе индексы часто опускаются, и векторы Uj, е, г, и Sj зачастую обозначаются как U, е, г и S. Читателю следует помнить, что для этих векторов индексы всегда подразумеваются, даже в тех случаях, когда они опущены для простоты записи.

R Л Пиыойыыо fSnnukiMO к-ппы л- i gt; gt; laquo;s

6.5. Возможность обнаружения и исправления ошибок

6.5.1. Весовой коэффициент двоичных векторов и расстояние между ними

Конечно же, понятно, что правильно декодировать можно не все модели ошибки. Возможности кода для исправления ошибок в первую очередь определяются его структурой. Весовой коэффициент Хэмминга (Hamming weight) w(U) кодового слова U определяется как число ненулевых элементов в U. Для двоичного вектора это эквивалентно числу единиц в векторе. Например, если 11=100101 101, то w(U) = 5. Расстояние Хэмминга (Hamming distance) между двумя кодовыми словами U и V, обозначаемое как c?(U, V), определяется как количество элементов, в которых они отличаются.

и= 1 001 О 11 О 1 V = 01 1110 100 rf(U, V) = б

Согласно свойствам сложения по модулю 2, можно отметить, что сумма двух двоичных векторов является другим двоичным вектором, двоичные единицы которого расположены на тех позициях, которыми эти векторы отличаются.

U + V= 1 110 11001

Таким образом, можно видеть, что расстояние Хэмминга между двумя векторами равно весовому коэффициенту Хэмминга их суммы, т.е. rf(U, V) = w(U + V). Также видно, что весовой коэффициент Хэмминга кодового слова равен его расстоянию Хэмминга до нулевого вектора.

6.5.2. Минимальное расстояние для линейного кода

Рассмотрим множество расстояний между всеми парами кодовых слов в пространстве V . Наименьший элемент этого множества называется минимальным расстоянием кода и обозначается d. Как вы думаете, почему нас интересует именно минимальное расстояние, а не максимальное? Минимальное расстояние подобно наиболее слабому звену в цепи, оно дает нам меру минимальных возможностей кода и, следовательно, характеризует его мошность.

Как обсуждалось ранее, сумма двух произвольных кодовых слов дает другой элемент кодовых слов подпространства. Это свойство линейных кодов формулируется просто: если U и V - кодовые слова, то и W = U + V тоже должно быть кодовым словом. Следовательно, расстояние между двумя кодовыми словами равно весовому коэффициенту третьего кодового слова, т.е. d(l], V) = w(U + V) = w(W). Таким образом, минимальное расстояние линейного кода можно определить, не прибегая к изучению расстояний между всеми комбинациями пар кодовых слов. Нам нужно лишь определить вес каждого кодового слова (за исключением нулевого вектора) в подпространстве; минимальный вес соответствует минимальному расстоянию d. Иными словами, 4мп соответствует наименьшему из множества расстояний между нулевым кодовым словом и всеми остальными кодовыми словами.

368 Гпаиа R kauanuuno /пп1лг- raquo;поа1лло- uo/tl 1

6.5.3. Обнаружение и исправление ошибок

Задача декодера после приема вектора г заключается в оценке переданного кодового слова и,. Оптимальная стратегия декодирования может быть выражена в терминах алгоритма максимального правдоподобия (см. приложение Б); считается, что передано было слово и если

Я(ги,)= max P(rU). (6.41)

по всем

Поскольку для двоичного симметричного канала (binary symmetric channel - BSC) правдоподобие U, относительно г обратно пропорционально расстоянию между г и Ц, можно сказать, что передано было слово U если

rf(rU,)= min rf(rU.). (6.42)

по всем V J

Другими словами, декодер определяет расстояние между г и всеми возможными переданными кодовыми словами U после чего выбирает наиболее правдоподобное U для которого

d(T,lJ,) lt;d(r,Vj) для/,у = 1,...,М и /Vy, (6.43)

где М = 2* - это размер множества кодовых слов. Если минимум не один, выбор между минимальными расстояниями является произвольным. Наше обсуждение метрики расстояний будет продолжено в главе 7.

На рис. 6.13 расстояние между двумя кодовыми словами U и V показано как расстояние Хэмминга. Каждая черная точка обозначает искаженное кодовое слово. На рис. 6.13, а проиллюстрирован прием вектора ri, находящегося на расстоянии 1 от кодового слова U и на расстоянии 4 от кодового слова V. Декодер с коррекцией ошибок, следуя стратегии максимального правдоподобия, выберет при принятом векторе Г] кодовое слово U. Если г, получился в результате появления одного ошибочного бита в переданном векторе кода U, декодер успешно исправит ошибку. Но если же это произошло в результате 4-битовой ошибки в векторе кода V, декодирование будет ошибочным. Точно так же, как показано на рис. 6.13, б, двойная ошибка при передаче U может привести к тому, что в качестве принятого вектора будет ошибочно определен вектор Гг, находящийся на расстоянии 2 от вектора U и на расстоянии 3 от вектора кода V. На рис. 6.13, в показана ситуация, когда в качестве принятого вектора ошибочно определен вектор Гз, который является результатом тройной ошибки при передаче и находится на расстоянии 3 от вектора кода U и на расстоянии 2 от вектора V. Из рис. 6.13 видно, что если задача состоит только в обнаружении ошибок, а не в их исправлении, то можно определить искаженный вектор - изображенный черной точкой и представляющий одно-, двух-, трех- и четырехбитовую ошибку. В то же время пять ошибок при передаче могут привести к приему кодового слова V, когда в действительности было передано кодовое слово U; такую ошибку невозможно будет обнаружить.

Из рис. 6.13 можно видеть, что способность кода к обнаружению и исправлению ошибок связана с минимальным расстоянием между кодовыми словами. Линия решения на рисунке служит той же цели, что и в процессе демодуляции, - для разграничения областей решения.

б R Втмпжнпптк пГлняпужрнма м ипппявления ошибок 369