 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Сигналы и спектры
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 [ 116 ] 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358
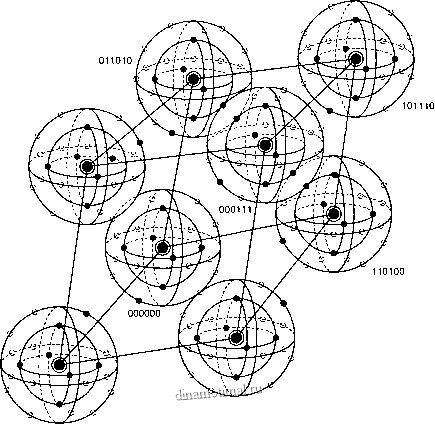
ния в этом примере не рассматриваются. Для каждого кодового слова два показанных слоя заняты искаженными кодовыми словами. На каждой внутренней сфере существует шесть таких точек (всего 48 точек), представляющих шесть возможных однобитовых ошибок в векторах, соответствующих каждому кодовому слову. Эти кодовые слова с однобитовыми возмущениями могут быть соотнесены только с одним кодовым словом; следовательно, такие ошибки могут быть исправлены. Как видно из нормальной матрицы, приведенной на рис. 6.11, существует также одна двухбитовая модель ошибки, которая поддается ис-
правлению. Всего существует j разных двухбитовых моделей ошибки, которыми
может быть искажено любое кодовое слово, но исправить можно только одну из них (в нашем примере это модель ошибки 0 1 0 0 0 1). Остальные четырнадцать двухбитовых моделей ошибки описьшаются векторами, которые нельзя однозначно сопоставить с каким-либо одним кодовым словом; эти не поддающиеся исправлению модели ошибки дают векторы, которые эквивалентны искаженным векторам двух или большего числа кодовых слов. На рисунке все (56) исправимые кодовые слова с одно- и двухбитовыми искажениями показаны маленькими черными кругами. Искаженные кодовые слова, не поддающиеся исправлению, представлены маленькими прозрачными кругами.
110011
011101
101001
Рис. 6.14. Пример восьми кодовых слов в пространстве 6-кортежей
При представлении свойств класса кодов, известных как совершенные коды (perfect code), рис. 6.14 весьма полезен. Код, исправляющий ощибки в t битах, называется со-верщенным, если нормальная матрица содержит все модели ощибки из t или меньшего числа ошибок и не содержит иных образующих элементов классов смежности (отсутствует возможность исправления остаточных ошибок). В контексте рис. 6.14 совершенный код с коррекцией ошибок в t битах - это такой код, который (при использовании детектирования по принципу максимального правдоподобия) может исправить все искаженные кодовые слова, находящиеся на расстоянии Хэмминга t (или ближе) от исходного кодового слова, и не способен исправить ни одну из ошибок, находящихся на расстоянии, превышающем г.
Кроме того, рис. 6.14 способствует пониманию основной цели поиска хороших кодов. Предпочтительным является пространство, максимально заполненное кодовыми словами (эффективное использование введенной избыточности), а также желательно, чтобы кодовые слова были по возможности максимально удалены друг от друга. Очевидно, что эти цели противоречивы.
6.5.5. Коррекция со стиранием ошибок
Приемник можно сконструировать так, чтобы он объявлял символ стертым, если последний принят неоднозначно либо обнаружено наличие помех или кратковременных сбоев. Размер входного алфавита такого канала равен Q, а выходного - Q+1; лишний выходной символ назьшается меткой стирания (erasure flag), ши просто стиранием (erasure). Если демодулятор допускает символьную ошибку, то для ее исправления необходимы два параметра, определяющие ее расположение и правильное значение символа. В случае двоичных символов эти требования упрощаются - нам необходимо только расположение ошибки. В то же время, если демодулятор объявляет символ стертым (при этом правильное значение символа неизвестно), расположение этого символа известно, поэтому декодирование стертого кодового слова может оказаться проще исправления ошибки. Код защиты от ошибок можно использовать для исправления стертых символов или одновременного исправления ошибок и стертых символов. Если минимальное расстояние кода равно d,, любая комбинация из р или меньшего числа стертых символов может быть исправлена при следующем условии [6]:
, gt;p+l. (6.50)
Предположим, что ошибки не появляются вне позиций стирания. Преимущество исправления посредством стираний качественно можно выразить так: если минимальное расстояние кода равно dnm, согласно уравнению (6.50), можно восстановить ,-1 стирание. Поскольку число ошибок, которые можно исправить без стирания информации, не превышает ( lt;/,ш,- 1)/2, то преимущество исправления ошибок посредством стираний очевидно. Далее, любую комбинацию из а ошибок и у стираний можно исправить одновременно, если, как поккзано в работе [6],
J , gt;2a + Y+1. (6.51)
Одновременное исправление ошибок и стираний можно осуществить следующим образом. Сначала позиции из у стираний замещаются нулями, и получаемое кодовое слово декодируется обычным образом. Затем позиции из у стираний замещаются единицами, и декодирование повторяется для этого варианта кодового слова. После об-
работки обоих кодовых слов (одно с подставленными нулями, другое - с подставленными единицами) выбирается то из них, которое соответствует наименьшему числу ошибок, исправленных вне позиций стирания. Если удовлетворяется неравенство (6.51), то описанный метод всегда дает верное декодирование.
Пример 6.6. Коррекция со стиранием ошибок
Рассмотрим набор кодовых слов, представленный в разделе 6.4.3.
000000 110100 011010 101110 101001 011101 110011 000111
Пусть передано кодовое слово 110011, в котором два крайних слева разряда приемник объявил стертыми. Проверьте, что поврежденную последовательность ххООИ можно исправить.
Решение
Поскольку rfmn = р + 1 = 3, код может исправить р = 2 стирания. В этом легко убедиться из рис. 6.11 или приведенного выше перечня кодовых слов, сравнивая 4 крайних правых разряда ххООИ с каждым из допустимых кодовых слов. Действительно переданное кодовое слово - это ближайшее (с точки зрения расстояния Хэмминга) к искаженной последовательности.
6.6. Полезность нормальной матрицы
6.6.1. Оценка возможностей кода
Нормальную матрицу можно представлять как организационный инструмент, картотеку, содержащую все возможные 2 записи в пространстве п-кортежей, в которой ничего не упущено и не продублировано. На первый взгляд может показаться, что выгода от использования этого инструмента офаничена малыми блочными кодами, поскольку для кодов длиной более п = 20 пространство п-кортежей насчитывает миллионы элементов. Впрочем, даже для больших кодов нормальная матрица позволяет определить важные исходные характеристики, такие как возможные компромиссы между обнаружением и исправлением ошибок и пределы возможностей кода в коррекции ошибок. Одно из таких офаничений, называемое пределом Хэмминга [7], описывается следующим образом:
Количество бит четности: п- к gt; log2
+... + | ||||||
Количество классов смежности. 2
+... + | ||||||
(6.52,а)
(6.52,6)
Здесь величина . , определяемая уравнением (6.16), представляет число способов
выбора из п бит j ошибочных. Заметим, что сумма членов уравнения (6.52), находящихся в квадратных скобках, дает минимальное количество строк, которое должно присутствовать в нормальной матрице для исправления всех моделей ошибки, вплоть до f-битовых ошибок. Неравенство определяет нижнюю границу числа п-к бит четности (или 2 * классов смежности) как функцию возможностей кода в коррекции f-битовых ошибок. Аналогичным образом можно сказать, что неравенство дает верхнюю границу возможностей кода в коррекции г-битовых ошибок как