 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Сигналы и спектры
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 [ 122 ] 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358
Принятый Beicrop подается во входной регистр, в котором в исходном состоянии все разряды имеют нулевое значение. После того как весь принятый вектор будет занесен в регистр сдвига, содержимое регистра - это и есть синдром. Теперь ключ 1 открывается, а ключ 2 закрывается, так что вектор синдрома теперь можно извлечь из регистра. Описанная последовательность действий имеет следующий вид.
Принятый вектор Ч У
10 0 10 11
Переключатель 1
Переключатель 2
Исходящий синдром
Рис. 6.20. Пример вычисления синдрома с помощью (п - к)-разрядного регистра сдвига Входная очередь Номер сдвига Содержимое регистра
1001011
100101
10010
1001
ООО Синдром
Если вектор синдрома нулевой, считается, что принятый вектор является правильным кодовым словом. Если синдром отличен от нуля, значит, обнаружена ошибка и принятый вектор - это искаженное кодовое слово; данная ошибка исправляется путем прибавления к принятому вектору вектора ошибки (указанной синдромом), т.е. аналогично процедуре, описанной в разделе 6.4.8. Этот метод декодирования хорош для простых кодов. Более сложные коды для практического использования требуют применения алгебраических методик.
6.8. Известные блочные коды
6.8.1. Коды Хэмминга
Коды Хэмминга (Hamming codes) - это простой класс блочных кодов, которые имеют следующую структуру:
(л,/:) = (2 -1,2 -1-/и).
(6.71)
где /и = 2,3,... . Минимальное расстояние этих кодов равно 3, поэтому, согласно уравнениям (6.44) и (6.47), они способны исправлять все однобитовые ошибки или определять все модели ошибки из двух или малого числа ошибок в блоке. Декодирование с помощью синдромов особенно хорошо подходит к кодам Хэмминга. Фактически синдром можно превратить в двоичный указатель местоположения ошибки [5]. Хотя коды Хэмминга не являются слишком мощными, они принадлежат к очень ограниченному классу блочных кодов, называемых совершенными; их особенности описывались в разделе 6.5.4.
Если предположить, что используется жесткое декодирование, вероятность появления битовой ошибки можно записать с помошью уравнения (6.46):
(6.72)
Здесь р - вероятность ошибочного приема канального символа (вероятность перехода в дюичном симметричном канале). Для отдельных кодов коррекции ошибок (таких как коды Хэмминга) вместо уравнения (6.72) мы можем использовать другое эквивалентное уравнение (это уравнение (Г. 16), которое выводится в приложении Г):
Рв-р-ра-рГ. (6.73)
На рис. 6.21 приведен график зависимости вероятности ошибки в декодированном бите от вероятности ошибки в канальном символе, на котором сравниваются разные блочные коды. Для кодов Хэмминга на фафике взяты значения /и = 3, 4 и 5 или (л, к) = (7, 4), (15,11), (31, 26). Для описания гауссового канала с использованием когерентной демодуляции сигналов BPSK, вероятность ошибки в канальном символе можно выразить через EJNo, как это бьшо сделано в уравнении (4.79):
P = Q
(6.74)
10-2
Код Хэмминга (31,26) f = 1 Код Хэмминга (15, 11)f = 1 Код Хэмминга (7,4) f = 1
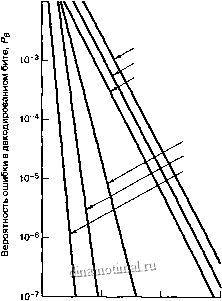
Расширенный код Голея (24,12) f = 3 КодБХЧ(127,64)Г=10 Код БХЧ (127, 36) f= 15
10- 10-2 ,0-3 10-*
Вероятность ошибочного приема канального символа, р
Рис. 6.21. Зависимость вероятности битовой ошибки от вероятности ошибки в канальном символе для нескольких блочных кодов
Здесь EJNq - отношение энергии кодового символа к спектральной плотности мощности шума, а Q{X) определено в уравнении (3.43). Чтобы связать EJNq с энергией бита информации на единицу плотности спектрального щума ( * Vo), используем следующее выражение:
Для кодов Хэмминга уравнение (6.75) принимает следующий вид:
1 = Nn
2 -1-т
2 -1
(6.75)
(6.76)
Объединяя уравнения (6.73), (6.74) и (6.76), Рв при когерентной демодуляции сигналов BPSK в гауссовом канале можно выразить как функцию EJNo. Результаты для различных типов блочных кодов отображены на рис. 6.22. Для кодов Хэмминга взяты следующие значения (л, к) = (7, 4), (15, И), (31, 26).
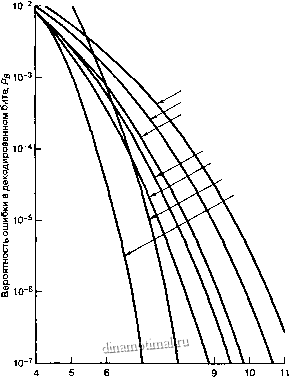
Некодированная передача Код Хэмминга (7, 4), f = 1 КодХэмминга(15,11),f=1
Код Хэмминга (31, 26), f = 1 Расширенный код Голея (24,12), f = 3 КодБХЧ(127,36),Г=15 КодБХЧ(127, 64),/=10
7 8 ь/Л/о(дБ)
Рис. 6.22. Зависимость Рв от Ei/No при когерентной демодуляции сигналов BPSK в гауссовом канале для нескольких блочных кодов