 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Сигналы и спектры
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 [ 149 ] 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358
Таблица 8.3. Таблица умножения для GF(8) приДЛГ) = 1+Х + Х
а raquo; | |||||||
8.1.4.4. Простой тест для проверки полинома на примитивность
Существует еще один, чрезвычайно простой способ проверки, является ли полином примитивным. У нередуцируемого полинома, который является примитивным, по крайней мере, хотя бы один из корней должен быть примитивным элементом. Примитивнъш элементом называется такой элемент поля, который, будучи возведенным в более высокие степени, даст все ненулевые элементы поля. Поскольку данное поле является конечным, количество таких элементов также конечно.
Пример 8.2. Примитивный полином должен иметь, по крайней мере, хотя бы один примитивный элемент
Найдите m = 3 корня полинома ДХ) = 1 + X + Х и определите, примитивен ли полином. Для этого проверьте, имеется ли среди корней полинома хотя бы один примитивный элемент. Каковы корни полинома? Какие из них примитивны?
Решение
Корни будут найдены прямым перебором. Итак, аР= 1 не будет корнем, поскольку ДаР)= 1. Теперь, чтобы проверить, является ли корнем а, воспользуемся табл. 8.2. Поскольку Да) = 1 + а + а = 1 + аР = О, значит, а будет корнем полинома. Далее поверим, будет ли корнем а. Да) = 1 + а+а=1 + аР = 0. Значит, и а также будет корнем полинома. Теперь проверим а. Да) = 1 + а + а = 1 + а = cd ?t 0. Следовательно, а корнем полинома не является. Будет ли корнем ос*? До*) = а + ос* + 1 = 1 + аР = 0. Да, ос* будет корнем полинома. Значит, корнями полинома ДХ) = 1 Н-Х + Х будут а, а и О*. Нетрудно убедиться, что последовательно возводя в степень любой из этих корней, можно получить все 7 ненулевых элементов поля. Таким образом, все корни будут примитивными элементами. Поскольку в определении требуется, чтобы по крайней мере один из корней был примитивным, полином является примитивным.
В этом примере описан относительно простой метод проверки полинома на примитивность. Для проверяемого полинома нужно составить регистр LFSR с контуром обратной связи, соответствующим коэффициентам полинома, как показано на рис. 8.8. Затем в схему регистра следует загрузить любое ненулевое состояние и выполнять за каждый такт правый сдвиг. Если за один период схема сгенерирует все ненулевые элементы поля, то данный полином с полем GF(2 ) будет примитивным.
8.1.5. Кодирование Рида-Соломона
В уравнении (8.2) представлена наиболее распространенная форма кодов Рида-Соломона через параметры п, к, t vi некоторое положительное число ш gt; 2. Приведем это уравнение повторно:
(n,Jt) = (2 -l,2 -l-20. (8.20)
Здесь n-k = 2t - число контрольных символов, а t - количество ошибочных битов в символе, которые может исправить код. Генерирующий полином для кода Рида-Соломона имеет следующий вид:
g W =8o + 8iX + gX + ...+g2,-iX-+ X. (8.21)
Степень полиномиального генератора равна числу контрольных символов. Коды Рида-Соломона являются подмножеством кодов БХЧ, которые обсуждались в разделе 6.8.3 и показаны в табл. 6.4. Поэтому связь между степенью полиномиального генератора и числом контрольных символов, как и в кодах БХЧ, не должна оказаться неожиданностью. В этом можно убедиться, подвергнув проверке любой генератор из табл. 6.4. Поскольку полиномиальный генератор имеет порядок 2t, мы должны иметь в точности 2t последовательные степени а, которые являются корнями полинома. Обозначим корни g(X) как: ос, а?, а. Нет необходимости начинать именно с корня а, это можно сделать с помощью любой степени а. Возьмем к примеру код (7, 3) с возможностью коррекции двухсимвольных ошибок. Мы выразим полиномиальный генератор через 2t = n-k = 4 корня следующим образом:
g(X) = (X - а)(Х - а) (X - а) (X - а*) =
= (Х - (а + а})Х + а?){Х - (а + а*)Х + а) =
= (Х - аХ + а)(Х - а*Х + а ) =
= Х* - (аЧ а*)Х + (а + а deg; + а deg;)Х - (а + а)Х + а =
= Х* - ах + а deg;Х - ах + .
Поменяв порядок расположения членов полинома на обратный и заменив знаки минус на плюс , так как нал двоичным полем +1 =-1, генератор g(X) можно будет представить следующим образом:
g(X) = a4ax + aV + ax4X. (8.22)
8.1.5.1. Кодирование в систематической форме
Так как код Рида-Соломона является циклическим, кодирование в систематической форме аналогично процедуре двоичного кодирования, разработанной в разделе 6.7.3. Мы можем осуществить сдвиг полинома сообщения ш(Х) в крайние правые к разряды регистра кодового слова и произвести последующее прибавление полинома четности р(Х) в крайние левые п-к разряды. Поэтому мы умножаем т(Х) на X *, проделав алгебраическую операцию таким образом, что ш(Х) оказывается сдвинутым вправо на л-А: позиций. В главе 6 это показано в уравнении (6.61) на примере двоичного кодирования. Далее мы делим Х *ш(Х) на полиномиальный генератор g(X), что можно записать следующим образом:
X - *ш(Х) = q(X)g(X) + р(Х). (8.23)
Здесь q(X) и р(Х) - это частное и остаток от полиномиального деления. Как и в случае двоичного кодирования, остаток будет четным. Уравнение (8.23) можно переписать следующим образом:
р(Х) = X ~*ш(Х) по модулю g(X). (8.24)
Результирующий полином кодового слова U(X), показанный в уравнении (6.64), можно переписать следующим образом:
U(X) = p(X) + X -m(X).
(8.25)
Продемонстрируем шаги, подразумеваемые уравнениями (8.24) и (8.25), закодировав сообщение из трех символов
010 ПО 111
с помощью кода Рида-Соломона (7,3), генератор которого определяется уравнением (8.22). Сначала мы умножаем (сдвиг вверх) полином сообщения а+осХ + аХ на Х * = Х, что дает аХ+аХ + оХ*. Далее мы делим такой сдвинутый вверх полином сообщения на полиномиальный генератор из уравнения (8.22), а+ аХ+ а deg;Х+ аХ + Х*. Полиномиальное деление недвоичных коэффициентов - это еще более утомительная процедура, чем ее двоичный аналог (см. пример 6.9), поскольку операции сложения (вычитания) и умножения (деления) выполняются согласно табл. 8.2 и 8.3. Мы оставим читателю в качестве самостоятельного упражнения проверку того, что полиномиальное деление даст в результате спедующий полиномиальный остаток (полином четности):
р(Х) = а + аХ + аХ + а*х1
Затем, из уравнения (8.25), полином кодового слова можно записать следующим образом:
U(X) = а + аХ + аХ + а*х + aV + ах* + ах*.
8.1.5.2. Систематическое кодирование с помощью (п -)-разрядного регистра сдвига
Как показано на рис. 8.9, кодирование последовательности из 3 символов в систематической форме на основе кода Рида-Соломона (7, 3), определяемого генератором g(X) из уравнения (8.22), требует реализации регистра LFSR. Нетрудно убедиться, что элементы умножителя на рис. 8.9, взятые справа налево, соответствуют коэффициентам полинома в уравнении (8.22). Этот процесс кодирования является недвоичным аналогом циклического кодирования, которое описывалось в разделе 6.7.5. Здесь, в соответствии с уравнением (8.20), ненулевые кодовые слова образованы 2 -1 = 7 символами, и каждый символ состоит из m = 3 бит.
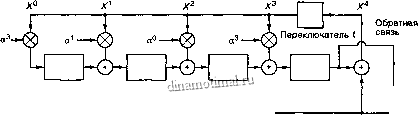
Выходная
последовательность (I символов сообщения
Входная последовательность символов сообщения 010 110 111 -
Переключатель 2
а а- а-
Рис. 8.9. Кодер LFSR для кода (7, 3)