 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Сигналы и спектры
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 [ 314 ] 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358
в тракте может быть весьма большим. Измерения показали, что для любых значений d потери в тракте Lp являются случайной переменной, имеющей логарифмически нормальное распределение в окрестности среднего значения Lp{d)[l\. Таким образом,
потери в тракте Lp можно выразить через Lp(d), введя в уравнение (15.6) случайную переменную Х.
Lp(d) (дБ) = LAdo) (дБ) + 10 и lg(d/do) + Х (дБ) (15.7)
Здесь Х обозначает случайную гауссову переменную с нулевым средним (в децибелах) со среднеквадратическим отклонением ст (также в децибелах). Х зависит от местоположения и расстояния. Поскольку Х, и Lp(d) - это случайные переменные, то, если для вычисления потерь в тракте или энергетического резерва линии связи использовать уравнение (15.7), предварительно нужно выбрать какое-то определенное значение Х . Часто выбор этого значения основывается на измерениях (сделанных для большого числа взаимных размешений приемника и передатчика). Обычные значения Х - это 6-10 дБ или даже выше. Таким образом, для статистического описания потерь в тракте вследствие крупномасштабного замирания при произвольном расположении с определенным расстоянием между передатчиком и приемником будут необходимы такие параметры: 1) эталонное расстояние, 2) показатель степени потерь в тракте и 3) среднеквадратическое отклонение Х . (Имеется несколько хороших работ, касающихся измерения и оценки потерь в тракте при распространении для различных приложений и конфигураций [1, 5-9].)
15.2.2. Мелкомасштабное замирание
В этом разделе будет рассмотрен компонент мелкомасштабного замирания го. Анализ проводится в предположении, что антенна движется по офаниченной траектории так, что влияние крупномасштабного замирания m(t) постоянно (и предполагается равным единице). Предположим, антенна перемещается и существует множество путей рассеивающих элементов, с каждым из которых связана переменная задержка распространения х (0 и переменный множитель a (t). Пренебрегая шумом, можно записать принятый полосовой сигнал следующим образом:
r(/) = 5]a (0[f-x (f)].
(15.8)
Подставляя уравнение (15.2) в (15.8), запишем принятый полосовой сигнал следующим образом:
r(t) = Re
= Re
5]a (r)g[r-x (0] е - 5]a (0e- g[r-x (r)]
(15.9)
Из уравнения (15.9) следует, что соответствующий принятый видеосигнал будет иметь следующий вид:
z(t) = 2]a (f)e-2 /A()g[, . (15.10)
Рассмотрим передачу немодулированной несущей на частоте /.. Иными словами, в любой момент времени g(r) = 1. Тогда для немодулированной несущей частоты и дискретных компонентов многолучевого распространения, выраженных в форме (15.10), принятый видеосигнал упростится до следующего вида:
г(г) = 2;;а (0е- =5]а (0- laquo; gt; , (I5.ll)
где 0 (г) = 2л/(.т (0. Видеосигнал г(0 состоит из суммы переменных ю времени векторов, имеющих амплитуду а (0 и фазу 0 (О. Следует отметить, что 0 (О будет изменяться на 2л радиан, когда т изменится на 1 . (обычно, это очень маленькая задержка). При работе сотового радиопередатчика на частоте /. = 900 МГц задержка I . равна 1,1 наносекунд. В свободном пространстве это соответствует изменению пути распространения сигнала на 33 см. Таким образом, в уравнении (15.11) 9 (0 может существенно измениться при относительно небольших изменениях задержки распространения. В этом случае, если два компонента многолучевого распространения сигнала отличаются по длине пути на 16,5 см, то один прибывающий сигнал будет отличаться по фазе от другого на 180 фадусов. Иногда векторы сигналов суммируются конструктивно, а иногда - деструктивно, что приводит в результате к изменениям амплитуды или замиранию z{t). Уравнение (15.11) можно записать более компактно в виде суммарной полученной огибающей, просуммированной по всем рассеивающим элементам.
2(0 = 0(06 * (15.12)
Здесь а(0 - результирующая амплитуда, а 9(0 - результирующая фаза. В правой части уравнения (15.12) представлен тот комплексный множитель, который ранее описывался в разделе 15.2. Уравнение (15.12) является важным результатом, поскольку из него видно, что хотя полосовой сигнал s{t), как показано в уравнении (15.2), подвержен замиранию, что приводит к приему сигнала lif), это замирание можно описать, анализируя г(0 на низкочастотном уровне.
На рис. 15.5 показан основной механизм, приводящий к замиранию в каналах с многолучевым распространением, как описывается уравнениями (15.11) и (15.12). На рисунке отраженный сигнал запаздывает по фазе (из-за увеличения расстояния рас-просфанения) относительно ожидаемого сигнала. Отраженный сигнал также имеет меньщую амплитуду (функция коэффициента офажения препятствия). Офаженные сигналы можно описать с помощью ортогональных компонентов д: (0 и у (0, где
A: (f) + iy (f) = a (f)e~ reg; * . Если количество таких стохастических компонентов велико и ни один из них не преобладает, то в фиксированный момент времени переменные xXt) и yXt), являющиеся результатом суммирования всех x if) и у (0, соответственно, будут иметь гауссову функцию распределения вероятностей. Эти ортогональные компоненты дают то же мелкомасштабное замирание го, которое бьшо определено в уравнении (15.4). При немодулированной несущей волне, как показано в уравнении (15.12), го(0 является модулем г(0
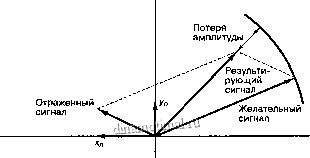
Рис. 15.5. Влияние многолучевого отражения сигнала на ожидаемый сигнал
Го(0 = л1хиО + Уг(0
(15.13)
Если полученный сигнал составлен из множественных отраженных лучей и значительного (незамирающего) компонента, распространяемого в пределах прямой видимости, амплитуда полученной огибающей имеет райсовскую функцию распределения плотности вероятности, показанную ниже, а замирание называют райсовским [2].
Р(Ь) =
jexp -
2о О
Го Л
дляго gt;0,А gt;0
для других Гц, Л
(15.14)
Хотя го(0 динамически изменяется во время движения, в любой фиксированный момент времени - это случайная переменная, которая является положительным действительным числом. Поэтому, описывая функцию плотности вероятности, можно опустить ее зависимость от времени. Параметр - это средняя мощность многолучевого сигнала до детектирования, А - максимальное значение незамирающего компонента сигнала (называемом зеркальным компонентом), а /о() - модифицированная функция Бесселя первого рода нулевого порядка [И]. Распределение Раиса часто записывают через параметр К, который определяется как отношение мощности зеркального компонента к мощности многолучевого сигнала. Математически это записывается как К = Al{2d). При приближении к нулю амплитуды зеркального компонента функция плотности вероятностей Раиса стремится к функции плотности вероятности Редея, имеющей следующий вид:
Р(Ь) =
ехр -
для Го gt; о для других Го
(15.15)
Релеевский замирающий компонент иногда называется случайным, рассеянным или диффузным, а плотность вероятности Редея является результатом отсутствия зеркального компонента сигнала; таким образом, для одиночной линии связи (без разнесения) она представляет собой функцию распределения вероятностей, связанную с наибольшим замиранием, приходящимся на среднюю мощность полученного сигнала.