 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Сигналы и спектры
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 [ 337 ] 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358
= W-fo)- (A.32)
Выше приведено свойство трансляции частоты, которое описывает смещенный
спектр, возникающий при умножении сигнала на е. Используя формулу (А.32) вместе с формулой (А.9), можно получить выражения для Фурье-образа сигнала, умноженного на косинусоиду.
a:(Ocos 2я/оГ = Ux(t)e - + x(t)e- -]
, (А.ЗЗ)
x(t)cos2nfot [X(f - /о) + X(f + fo)]
Данное свойство также называется теоремой о модуляции (или смешивании). Умножение произвольного сигнала на синусоиду частоты /о приводит к трансляции исходного спектра сигнала на /о и -/о.
А.4. Полезные функции
А.4.1. Дельта-функция
Полезной функцией в теории связи является так называемая дельта-функция Дирака, или единичный импульс, 8(/). Импульсную функцию можно получить из любой фундаментальной функции (например, прямоугольного или треугольного импульса). В любом случае импульсная функция определяется в пределе (амплитуда импульса стремится к бесконечности, длительность импульса - к нулю, а площадь импульса равна единице) [5]. Единичная импульсная функция имеет следующие свойства:
J8(t)dt = l, (А.34)
5(0=0 npHftO, (А.35)
6(0 не ограничена в точке t = 0, (А.Зб)
5{8(0}=г {5(/)} = 1, (А.37)
x(t)6(t-to)dt = x(to). (А.38)
Формула (А.38) представляет фильтрующее свойство; результат интегрирования произведения функции д:(0 с дельта-функцией - выборка функции x(t) в точке / = to.
В некоторых задачах полезными бывают следующие представления дельта-функции в частотной и временной областях:
8(0=р 4Г. (А.39)
8(/) =
-2пф
(А.40)
А.4.2. Спектр синусоиды
Для нахождения Фурье-образа синусоидального сигнала необходимо предположить, что данный сигнал существует только в интервале (-Туг lt; / lt; Т2). При таком условии функция будет иметь Фурье-образ, пока То будет конечно. В пределе То предполагается очень большим, но конечным. Спектр сигнала д:(/) = А cos 2nfy можно найти, используя формулы (А.9) и (А.26).
X{f) =
А 2 J
-27C,(/-/o)f ,-2JU(/+/o)f,
Как видно из формулы (А.40), данное интегральное выражение можно записать через следующие единичные импульсные функции:
Х(/) = [5(/-/о) + 8(/ + /о)].
(А.41)
Подобным образом можно показать, что спектр синусоидального сигнала y(f) = А sin 2%fy равен следующему:
П/)=-[8(/-/о)-8(/ + /о)].
(А.42)
Спектр косинусоидального сигнала показан на рис. А.6, а спектр синусоидального сигнала - на рис. А.7. Все дельта-функции на этих рисунках изображены как пики с весовыми коэффициентами А/2 или -А/2.
X(f)
1
-fo о fo
Рис. А.6. Спектр сигнала x(t) - А cos 2nfy
А.5. Свертка
В конце XIX века Оливер Хевисайд (Oliver Heaviside) использовал свертку для вычисления тока на выходе электрической схемы, на вход которой подан сигнал, описываемый сложной функцией напряжения. Использование методов Хевисайда предшествовало применению аналитических методов, разработанных Фурье и Лапласом (хотя публикации Фурье и Лапласа вышли раньше).
lY{f)
-A/2
Puc /4.7 Спектр сигнала y(t) = A sin iKfy
Отклик схемы на входное импульсное возмущение v(t) = 8(0 называется импульсной характеристикой и обозначается h(t), как показано на рис. А.8, т.е. это просто выходное напряжение, полученное при подаче на вход дельта-функции. Хевиса11Д аппроксимировал произвольный сигнал, подобный показанному на рис. А.9, а, набором равноотстоящих импульсов. Подобные импульсы конечной высоты и ненулевой длительности показаны на рис. А.9, б. В пределе при длительности импульса Ат- gt;0 каждый импульс стремится к дельта-функции с весовым коэффициентом, равным площади импульса. Далее будем считать, что данные равноотстоящие импульсы имеют нулевую длительность, хотя строго они являются такими только в пределе.
v{t) = b{t)
Вход
Линейная сеть
Выход
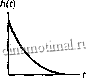
Рис. А.8. Импульсная характеристика линейной системы
Поскольку нас интересует как время подачи импульсов на вход, так и время наблюдения реакции на них на выходе, следует весьма аккуратно использовать обозначения различных величин, связанных со временем. Поэтому определим две различные временные последовательности; начнем с использования следующей формы записи.
1. Время на входе будем обозначать через т, так что входные импульсы напряжения будут записываться как v(t,), v(T2), v(T;v).
2. Время на выходе будем обозначать через /, так что выходные функции тока будут записываться как i(/i), /(/2), /(w)-
Хевисайд нашел отклик схемы (или ток на выходе) для каждого входного импульса; после этого он сложил эти токи и получил общий ток на выходе. Весоюй коэффициент прямоугольного импульса, поданного в момент т - это произведение v(Ti) At. Если устремить Ат к нулю, последовательность импульсов будет аппроксимировать произюльное входное напряжение настолько точно, насколько это нужно. Снова отметим, что момент подачи импульса на вход - это т а момент определения реакции системы - / где т - переменная входного времени, at-переменная выходного времени, i=l,...,N.