 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Сигналы и спектры
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 [ 350 ] 351 352 353 354 355 356 357 358
1-aiZ- 1-a2Z l-asZ
I-p1z-1 I-p2z-1
Puc. Д.6. Цифровой фильтр как последовательность каскадов прямой и обратной связи первого порядка
В данном выражении (и на рисунке) обособлены все блоки первого порядка, описываемые нулями и полюсами фильтра. Чтобы фильтр был устойчивым, модули всех полюсов (Р Р2, Рз) каскада должны быть меньше 1. Если хотя бы один блок первого порядка неустойчив (или расходится), неустойчивым является и весь каскад. Как отмечалось для преобразования Лапласа, полюса (и нули) г-области могут быть комплексными, поэтому в качестве критерия устойчивости используется их абсолютная величина, а не амплитуда. (Стоит сказать, что реализация поточного графа, представленная на рис. Д.б, - это всего лишь иллюстрация принципов анализа; реальный цифровой фильтр никогда не реализуется в подобной факторизованной форме, поскольку в этом случае некоторые множители могут быть комплексными, а это может повлечь за собой ненужное усложнение вычислительных требований фильтров.)
Д.3.4. Диаграмма полюсов-нулей и единичная окружность
Если комплексные нули и полюса фильтра или линейной системы изобразить на плоскости с действительной и мнимой осями, данную плоскость можно будет назвать г-плоскостью (или комплексной плоскостью). Система является устойчивой, если все ее полюса находятся внутри единичной окружности. На рис. Д.7 показан вид г-плоскости для следующей передаточной функции.
Мнимая часть
X Полюсы о Нули
z-плоскость
-1 I
.Действительная
часть
Рис. Д. 7. Полюсы и нули, изображенные на z-плоскости
п о ---1--
Я(г) =
1-2г +3г
(1-(1 + /У2)г )(1-(1-1л/2)г ) (1- (1/3 +1 л/2/3)г- )(1 - (1/3 - iy/2f3)z-)
(l-aiz )(l-a2Z-)
(Д.ЗЗ)
(l-PlZ-)(l-P2Z-)
Нули данной функции - z = 1 + iI2 и г = 1 - i V2 , полюсы - z = 1/3 + if2 /3 и z = 1/3 -
i-Jl / 3. Поскольку все полюсы лежат внутри единичной окружности, данный фильтр является устойчивым.
Д.З.5. Дискретное преобразование Фурье импульсной характеристики цифрового фильтра
Частотная характеристика цифрового фильтра вычисляется из дискретного преобразования Фурье (discrete Fourier transform - DFT, ДПФ) импульсной характеристики фильтра. Напомним вид преобразования Фурье, приведенного в формуле (А.26).
X(f)= Uoe-fidt (Д.34)
Данную формулу можно использовать для вычисления Фурье-образа импульсной характеристики фильтра. Ее можно упростить, полагая, что используется дискретная версия сигнала jt(0, причем выборка сигнала производится каждые Т; = l/f, секунд.
~ ов со
оо * = -оо к=-ос
Разумеется, импульсная характеристика цифрового фильтра является причинной, и первая выборка импульсной характеристики производится в момент = 0, а последняя - в момент k = N-l, что в сумме дает N выборок на одно преобразование. Таким образом, для данного конечного числа выборок можно переписать формулу (Д.25), использовав не явное время кТ а число выборок к.
X(if) = Y.(k)e- - f- (Д.36)
Отметим, что значение выражения (Д.36) вычисляется для непрерывной частотной переменной /. В действительности же нам требуется знать это значение для некоторых определенных частот - нулевой частоты (постоянной составляющей) и гармоник собственной частоты; всего N дискретных частот: О, /о, 2/о и так до где/о= ШГ,.
X() = Y,x(k)e- дляnот0доV- 1
(Д.37)
k = 0
Выражение выше можно упростить, использовав только временной индекс к и частотный индекс п. В результате получаем дискретное преобразование Фурье (discrete Fourier transform - DFT, ДПФ).
;v-i
X(n) = jt(fc)e- * для и от 0 до - 1
(Д.38)
* = о
Поскольку частота дискретизации сигнала х(к) равна /j выборок/с, сигнал включает воображаемые (или вымышленные) компоненты на частотах свыше fJ2. Следовательно, при вычислении значения выражения (Д.38) достаточно ограничиться частотами до /У2. Отметим, что формула (Д.38) аналогична формуле (Д.23), если положить z = g(2nm)m jjj, последовательности выборок длиной N.
Д.4. Фильтры с конечным импульсным откликом
На настоящий момент наиболее распространенный тип цифровых фильтров - это фильтры с конечной импульсной характеристикой (КИХ), имеющие, как понятно из названия, импульсный отклик конечной длительности. Данные фильтры не имеют весовых коэффициентов обратной связи (см. рис. Д.4); следовательно, можно сделать вывод о их безусловной устойчивости. Выход фильтра с КИХ, приведенного на рис. Д.8, описывается следующим выражением:
х(/с-1)
х(/с-2)
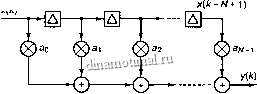
Рис. д.8. Цифровой фильтр с конечной импульсной характеристикой
у(к) = аох(к) + aix(k - 1) + а2х(к - 2) + азх(Л - 3) + ... + п/у- ixik - Л/ + 1) = а х{к-п) .(Д.39)
п = 0
Таким образом, передаточная функция фильтра имеет только нули и не имеет полюсов.
H(z) = ао + fliz +a2Z + a3Z +
.. + aN-\Z
(Д-40)
= ао(1 - а,г-)(1 - a2Z-)(l - азг-)...(1 - az )
По сути, работа фильтра с КИХ - это вычисление текущего среднего, когда выход - это взвешенное среднее N последних входных выборок. Таким образом, фильтры данного типа часто называются фильтрами скользящего среднего (moving average filter). Кроме того, их еще называют линиями задержки с отводами (tapped delay line) и трансверсальньши фильтрами (transversal filter).
л.4 chMnL.