 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Сигналы и спектры
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 [ 38 ] 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358
vfjit)vfAt)dt = Kj8jt 0 lt;t lt;T j,k=l,...,N,
(3.8,a)
где оператор
l Щ1я] = к О mijk
(3.8,6)
называется дельта-функцией Кронекера и определяется формулой (3.8,6). При ненулевых константах Kj пространство именуется ортогональным. Если базисные функции нормированы так, что все А;= 1, пространство называется ортонормированным. Основное условие ортогональности можно сформулировать следующим образом: каждая функция набора базисных функций должна быть независимой от остальных функций набора. Каждая функция \г/0 не должна интерферировать с другими функциями в процессе детектирования. С геометрической точки зрения все функции у/О взаимно перпендикулярны. Пример подобного пространства с N=3 показан на рис. 3.3, где взаимно перпендикулярные оси обозначены vfi(t), угС) и vfj(t). Если vf/t) соответствует действительному компоненту напряжения или силы тока сигнала, нормированному на сопротивление 1 Ом, то, используя формулы (1.5) и (3.8), получаем следующее выражение для нормированной энергии в джоулях, переносимой сигналом за Т секунд:
Ej =
WJit)dt = Kj.
(3.9)
2(0
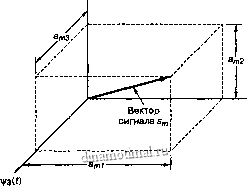
Рис. 3.3. Векторное представление сигнала s {i)
Одной из причин нащего внимания к ортогональному сигнальному пространству является то, что в нем проще всего определяется Евклидова мера расстояния, используемая в процессе детектирования. Стоит отметить, что даже если переданные сигналы формируют подобного пространства, они могут преобразовываться в линейную комбинацию ортогональных сигналов. Можно показать [3], что произвольный конечный набор сигналов {s,it)} (/= 1,М), где каждый элемент множества физически
реализуем и имеет длительность Т, можно выразить как линейную комбинацию N ортогональных сигналов YiO), 2(0, Wrt), где N lt;M, так, что
Slit) = 021VKO + 0222(0 + + aiNWM
SmU) = CMllit) + ам22{1) + + aMNNit)
Эти соотношения можно записать в более компактной форме:
Si(t) = 5] laquo;yV/) = 1. Л/, (3.10)
; = 1
N lt;M,
а,: =
Siit)\\fj(t)dt i=l, ...,М 0 lt;t lt;T, (3.11)
Oij - это коэффициент при у/г) разложения сигнала s,(f) по базисным функциям. Вид базиса не задается; эти сигналы выбираются с точки зрения удобства и зависят
от формы переданных сигналов. Набор таких сигналов {s,(0} можно рассматривать как набор векторов { laquo;Л = [а, an,ajs). Если, например, N = 3, то мы можем изобразить вектор s , соответствуюший сигналу
sM = a; iyi(0 + a 22it) + атзУз(0 gt;
В виде точки в трехмерном Евклидовом пространстве с координатами (ai, а 2, о з), как показано на рис. 3.3. Взаимная ориентация векторов сигналов описывает связь между сигналами (относительно их фаз или частот), а амплитуда каждого вектора набора {s} является мерой энергии сигнала, перенесенной в течение времени передачи символа. Вообще, после выбора набора из Л ортогональных функций, каждый из переданных сигналов Si(t) полностью определяется вектором его коэффициентов:
S, = а,2,аш) i= I,М. (3.12)
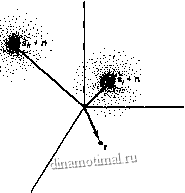
В дальнейшем для отображения сигналов в векторной форме будем использовать запись {s} или {s(f)}. На рис. 3.4 в векторной форме (которая в данном случае является очень удобной) показан процесс детектирования. Векторы s, и представляют сигналы-прототипы, или опорные сигналы, принадлежащие набору из М сигналов, {Sj{t)]. Приемник априори знает местонахождение в пространстве сигналов всех векторов-прототипов, принаддежащих М-мерному множеству. В процессе передачи каждый сигнал подвергается воздействию шумов, так что в действительности принимается искаженная версия исходного сигнала (например, s,- + п или + п), где п - вектор помех. Будем считать, что помехи являются аддитивными и имеют гауссово распределение; следовательно, результирующее распределение возможных принимаемых сигналов - это кластер или облако точек вокруг и sj. Кластер сгущается к центру и
разрежается с увеличением расстояния от прототипа. Стрелочка с пометкой г представляет вектор сигнала, который поступает в приемник в течение определенного интервала передачи символа. Задача приемника - определить, на какой из прототипов М-мерного множества сигнал похож больше. Мерой сходства может быть расстояние. Приемник или детектор должен решить, какой из прототипов сигнального пространства ближе к принятому вектору г. Анализ всех схем демодуляции или детектирования включает использование понятия расстояние между принятым сигналом и набором возможных переданных сигналов. Детектор должен следовать одному простому правилу, определять принадлежность г к тому же классу, к которому принадлежит его ближайший сосед (ближайший вектор-прототип).
2(t)
VI (t)
V3(f)
Рис. 3.4. Сигналы и шум в трехмерном векторном пространстве
3.1.3.1. Энергия сигнала
С помощью формул (1.5), (3.10) и (3.8) нормированную энергию Е связанную с сигналом s,(0 в течение периода передачи символа Т, можно выразить через ортогональные компоненты s,(0:
о о\ j
о J *
j к о
J к
(3.13) (3.14) (3.15) (3.16)